Finally the 121st edition of Carnival of Mathematics, a great idea of The Aperiodical!! I am extremely exited to host this. In case you don’t know much about this carnival I encourage you to read more The Aperiodical and maybe you could be the next host. So, lets get started! ^_^
 Understanding 121: Firstly, 121 is not prime because it is the square of 11 (thus it is a composite number). And it is an odd number.
Understanding 121: Firstly, 121 is not prime because it is the square of 11 (thus it is a composite number). And it is an odd number.
An interesting fact is that 121 is the sun of three consecutive primes: 37 + 41 + 43. Another fascinating thing about 121 is that there are no squares besides 121 known to be of the form  , where p is prime, in our case 3 (because 1 + 3 + 9 + 27 + 81 = 121). Other such squares must have at least 35 digits. Moreover, 121 is special because there are only two other squares known to be of the form n! + 1 ( because 5! + 1 = 120 + 1 = 121).
, where p is prime, in our case 3 (because 1 + 3 + 9 + 27 + 81 = 121). Other such squares must have at least 35 digits. Moreover, 121 is special because there are only two other squares known to be of the form n! + 1 ( because 5! + 1 = 120 + 1 = 121).
Now the maths posts, but first thank you very much for all the posts submitted to us.
- In the article “The Brilliant M.C. Escher in 7 Pictures“, The Maths Book shows us some great mathematics art by Escher and the different ways he incorporates mathematics into his artwork.. Wonderful works of art full of great geometry principles and not only.
- In the article “Probability Tends to Zero“, we have the personal experience of Ùr-Fhàsaidh: an interesting explanation of what happens to children after important festivities such as Christmas and Easter (the author names these: Christmas Month Effect and Easter Month Effect ) in Ireland, where mathematics plays an important role as it is required for admission to college and university.
- In the article “Extremely Small Probabilities“, the author John D. Cook talks about normal probability distribution, which can predict negative values of things that cannot be negative (such as women with negative height) . But in practice these probabilities can be so incredibly small that other things matter more. An interesting article that teaches us some interesting things about small probabilities.
- More probabilities in the article “Why isn’t everything normally distributed?” by John D. Cook gives us more insight into normal distribution and the central limit theorem, which explains why many things have a normal (Gaussian) distribution.
- In the article “We’re Judgmental Jerks When We Say “I Don’t Get It”, the author Math Misery? gives and interesting and understandable description of how we (students or instructors/teachers) handle the oft-repeated phrase, “I don’t get it”. It is a problem most of us encountered at many levels and ages. In general this problem is about understanding what we were anticipating for the subject/lecture/theory presented.
- In the post “Puzzling Grades“ by Tanya we have an interesting problem regarding grading students at university. Being a student, I had the same problem understanding the grading system. Take a look at the problem and see if you can spot the cause of the problem.
- The article “What’s so Great about Continued Fractions“ by Scientific American presents some great properties of continued fractions ( fractions made of fractions) and also it contains examples such as Pi.
- The article “Which sequence is more likely to appear first: HTT or HTH?” talk about the problem of coin – flips and how we can get HTT or HTH with interesting experiments and computer programs. The article is more interactive because it has multiple videos in it where the author and his children discuss the problem.
- The post “Where’s the Function?” by cavmaths presents a function related problem and emphasizes the importance the graph plays in understanding the function. Sometimes, we don’t need to know the algebraic form of the function to answer a question, the graph gives us a lot of information. Also, the article gives students a nice tip for exam revision.
- The article “Thoughts About Inscribed Angles and Arcs” by ( x, why? ) discusses some interesting tricks and tips for teachers for a geometry lesson on inscribed angles. Sometimes it is tricky to understand all the ways an inscribed angle can appear in a circle.
- The article “Emmy the student and Emmy the communist!” by The Renaissance Mathematicus gives some interesting insights into the life of Emmy Noether, some that you cannot find in general articles, or are understood poorly.
- The post “A Galactic Prize” gives us some interesting concepts on how to understand formulas. As the author Matifutbol says about the article: “The mathematical language is so amazing that, with a few figures, and a pair of operations, we can create formidable numbers. The problem comes in how to calculate them.”
- The post “You Down With WODB? Yeah You Know Me!” the author (Nora) discusses an interesting activity that she has done with her students in class. It is a good project to do in class and it is helpful for students understand mathematical concepts.
And this is the end of the Carnival. Hope you enjoyed it, because it was a great experience for me and I am thinking of hosting it again. If you want to be a host click here. And also check the next carnival posts. The #122 edition will be hosted by Solve My Maths.
Thank you for reading. Have a great weekend. Wish you the best and don’t forget that maths is everywhere. ^_^
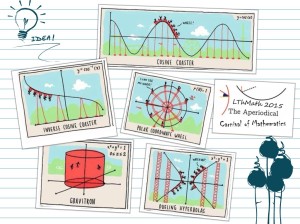

If I’m not mistaken the wonderful pictures of mathematical-function amusement park rides are from a strip by Grant Snider, whose Incidental Comics is almost a parade of poster-worthy drops of joy. Many are mathematical, many are artistic; I can’t read enough of them.
LikeLike
You are 100% right 🙂 They are awesome 🙂 And I thought they worked perfect for the occasion ^_^
LikeLike
Sorry I missed this call! How about this post from Grandma got STEM? https://ggstem.wordpress.com/2015/01/17/joanne-growney/
LikeLike
This is a nice article, but you can still submit it to the next edition and they could post it. Just follow the above (mentioned) link for The Aperiodical and you will find out how to submit them.
LikeLike