The Sea Island Mathematical Manual

I was never knew a lot of things about how mathematics evolved in China and a couple of days ago I have found this incredible picture on Tumblr: Illustration of Liu Hui’s sea island survey methods. Published in 263 AD as an appendix to The Nine Chapters on the Mathematical Art, Liu Hui constructed mathematical proofs for many practical applications of geometric principles

All of these deserve a little more and so I started to look for more. The internet is full of knowledge, so here is what I found. The book ‘The Nine Chapters on the Mathematical Art’ is a Chinese maths book developed in centuries by generations of scholars from the 10th–2nd century BCE. I found incredibly interesting and beautiful the fact that they called it Mathematical Art – it gives us the exact idea of how they understood and perceived this topic, even if the book had practical applications (as you can see in the picture above). It seems that some of the methods used in the book were not completely understood in the European community. For example, the method of chapter 8 uses Gaussian elimination before Carl Friedrich Gauss (1777–1855), which makes things quite interesting. I find these things fascinating, and I always feel that the way nations and countries cooperate now is such a big bonus and that we should totally do this more. We will develop more like this.

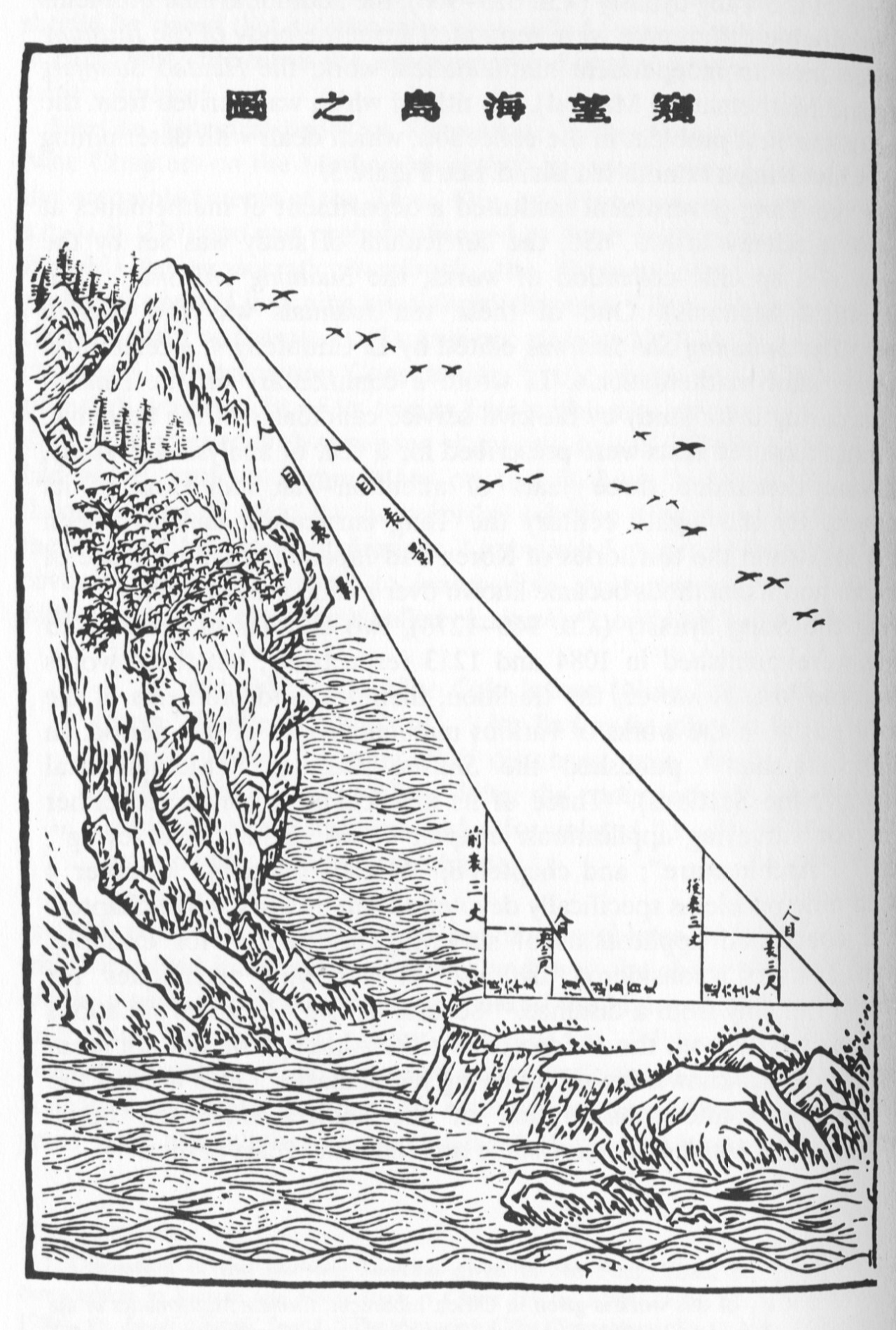
‘The Sea Island Mathematical Manual’  is just an extension of chapter 9 of the book mentioned above, but it is written by mathematician Liu Hui. At some point (during the Tang Dynasty) this was made into a separate book, and it was selected as the official mathematical text for imperial examinations in mathematics. It had a lot of geometric applications and it was considered extremely useful. Everything came from the following problem:

Q: Now surveying a sea island, set up two three zhang poles at one thousand steps apart, let the two poles and the island in a straight line. Step back from the front post 123 steps, with eye on ground level, the tip of the pole is on a straight line with the peak of island. Step back 127 steps from the rear pole, eye on ground level also aligns with the tip of pole and tip of island. What is the height of the island, and what is the distance to the pole ?

A: The height of the island is four li and 55 steps, and it is 120 li and 50 steps from the pole.

As you can observe it was extremely important for navigation and also geographical perspectives. If you want to find out more about this you can check Wikipedia – The Sea Island Mathematical Manual. Also, if you want to read the book, Frank Swetz provides an annotated translation of the Haidao (a testimony to the ingenuity and skill of China’s early surveyors and its author, Liu Hui) and an analysis of its surveying problems. In particular, he details surveying techniques and undertakes a mathematical exposition of the Chinese chong cha solution procedures.The book is The Sea Island Mathematical Manual: Surveying and Mathematics in Ancient China; I have not read it yet, but I believe it should be on my reading list (which, just between the two of us, it starts to become so incredibly big) and also on anyone’s interested in history of mathematics and Chinese knowledge of that time.

Let me know if you would like to read my opinion about Liu Hui in another post especially dedicated to him and his breakthroughs – I would like to write about him. You can see a representation with him in the following stamp-picture:

Hope you had a great day. Enjoy the rest of the weekend. Thank you for reading and enjoy your week. You can find me on Facebook,  Tumblr,  Google+,   Twitter  and  Instagram. Don’t forget that maths is everywhere!